Properties of the Centroid
By: Sydney Roberts
A median is a line segment that
extends from the vertex of a triangle to the midpoint of the opposite side of
the triangle. Therefore, each triangle with have three medians that intersect
at a point that is exactly two-thirds of the way along each median from each
vertex. We call this point the Centroid.
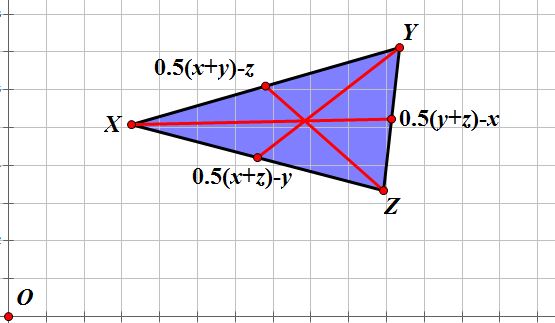
How do we know this is true? Consider
the following triangle XYZ.
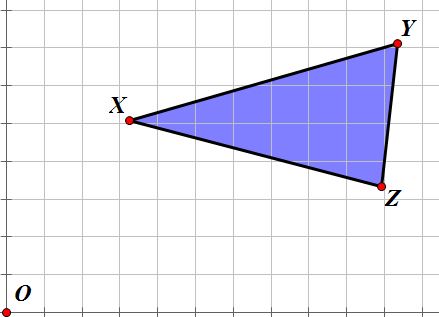
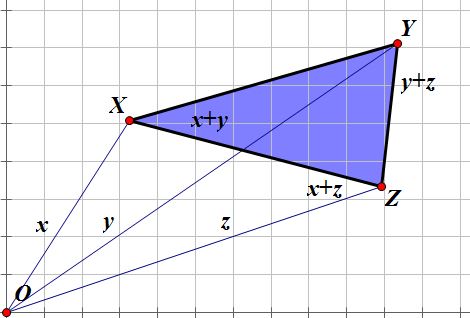
We can think of each vertex of this
triangle as a vector. Hence, we can label each side as such, where x is the vector extending from O to X, y is the vector extending from O to Y,
and similarly z is the vector
extending from O to Z.
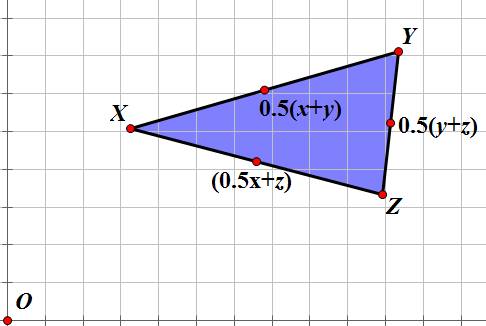
Now, hiding the original vectors in
order to avoid clutter, we can also find the midpoints of each side of the
triangle and label them as such.
Now that we have the midpoints, we
can construct the medians.
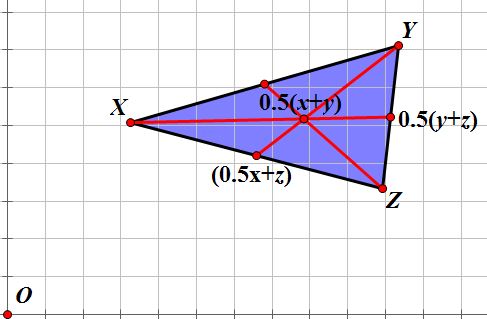
Now we want to show that each of
these medians intersect at a common point. Specifically, we want to show that
these medians intersect at the point 
which we refer to as the centroid
of a triangle. As mentioned before, we want to show that this centroid lies two-thirds of the
way down each median from the vertex. Well, now that we have the vectors for
each side length, we can label the medians as follows.
Now we just need to show that
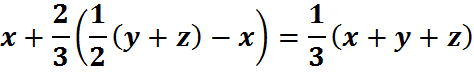
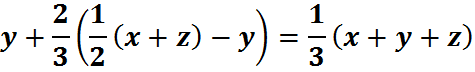
And
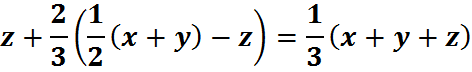
Well,
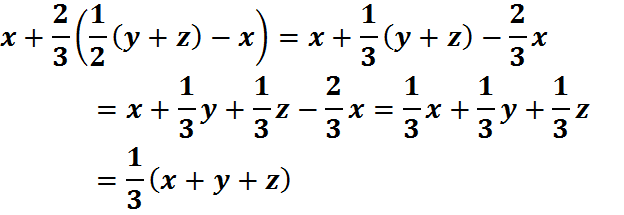
Similarly, this algebra will hold on the
remaining two equations and we see that the centroid
does indeed lie at a point two-thirds of the way along each median from the
vertex.
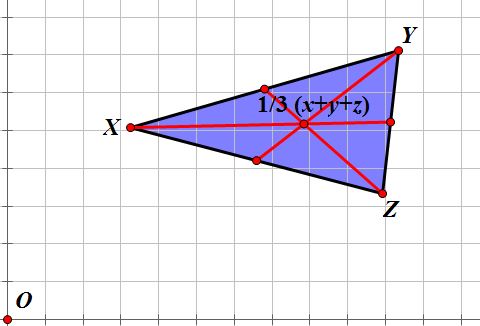
The centroid is
commonly referred to as the “center of mass” or “center of gravity” for a
triangle. This idea comes from the fact that if you had a 2D triangle with the centroid labeled, that this centroid
would be the balancing point and the triangle could rest on this point alone
without toppling. This should only work if the area around this point is evenly
dispersed.
Therefore, consider the three triangles
that are formed by the intersection of the medians.
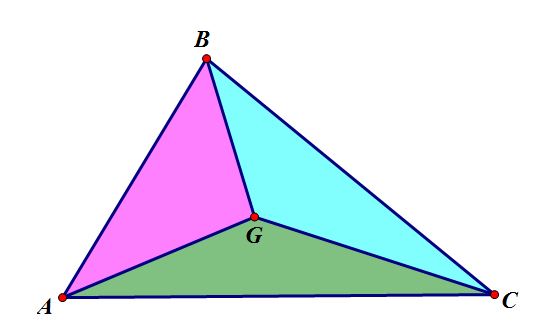
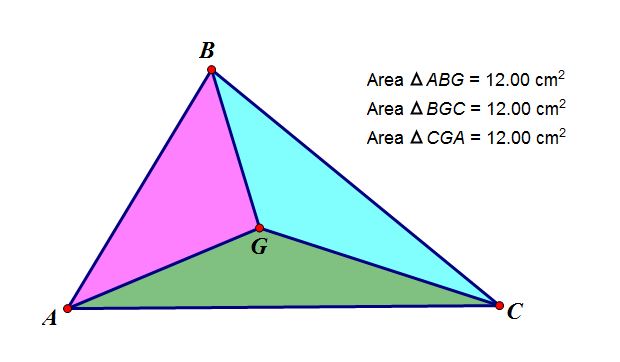
Now we want to show that the area of
triangle ABG equals the area of triangles CGA and BGC. Conveniently, we can use
Geometer’s Sketchpad to calculate this, and we can see that this is true.
If you want to change the triangle and
see that the areas remain equal, use the following GSP file: